Mathematics of sudoku

I've been doing the Metro News sudoku lately. I got thinking about the math in sudoku and the sudoku problem space. There's enough in there to make a high school level math problem or two.

Now the sudoku puzzles promise there's no math involved. And that's true. Although it's a 9x9 grid of numbers, the use of 1-9 is a convenience. Any set of 9 distinct symbols would work. You could use 9 Egyptian hieroglyphs, or the first 9 letters of the Greek alphabet and it would work the same and still be a sudoku.

I got thinking about the total problem space. How many ways are there to arrange 9 rows of the numbers 1-9. well that's not too hard to calculate. there are 9 factorial, 9! ways to arrange any row. so 362,880 ways a set of 9 symbols can be arranged.

The "first" or "bottom" row requires some consideration. I originally thought there were 9! ways to arrange the first row. I'm now pretty sure there is just one way to create the first row based on the definition

The first row consists of the 9 distinct symbols in any order. For convenience the symbols can be labeled S₁, S₂, S₃, ... S₉

Thus there is actually only one way to arrange the bottom row. For subsequent rows the actual symbols in the rows below matter so the usual combinatrics should apply.

Now in the total problem space each row is independent, so the total number of 9 cell rows above the first row is 9!⁸ which is 300,679,807,141,676,000,000,000,000,000,000,000,000,000,000 or about 10⁴⁴.

Now within this space only some of the arrangements will be valid sudoku. I was thinking how many sudoku are there, and how sparse within the total problem space are arrangements which are valid sudoku. I knew it would be sparse. Think about it this way. Working from the bottom row up, suppose you have 8 rows filled in. Then for the final top row there is just one way out of 362,880 to arrange the top numbers so that the result is a sudoku. This is because at each point along the top row the 8 numbers "below" will be filled, leaving only one possible number that can go into each of the 9 slots along the top, thus there is only 1 way to build the top row given 8 sudoku compliant rows below.

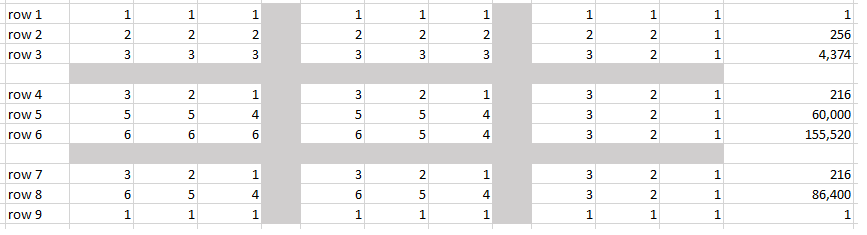
I was able to work out an upper bound on the number of sudoku there can be. I used the method of going left to right, bottom to top. Note again, there is only 1 way to fill in the bottom row. At each point I determined the optimistic maximum number of available numbers there could be, based on how many numbers were filled in to the left, below, or within the 3x3 subgrid. For example in the third row up, 7 numbers in, there are two numbers below filled, 6 numbers to the left filled, 0 within the 3x3 grid filled. so there are optimistically 3 numbers available that can go into this slot.

Now this is optimistic counting as it assumes that the smaller sets of numbers are proper subsets of the larger set used to determine the size of available numbers. Again this is an upper bound ballpark calculation. so filling it in the grid ended up looking like this

when you multiply the number from each row together it comes out to 42,118,945,229,525,500,000,000,000 or about 10²⁵.

dividing the numbers we can see how sparse the sudoku solutions are within the total space, only 1 in 7,138,825,663,917,590,000  arrangements of the 9x9 number grid is a sudoku. so 7 x 10¹⁸, or 1 in 7 billion billion. so it's pretty sparse.